格密码基础知识
格密码1.1 格
本笔记来自于本人对网上各种关于格密码内容的整理,可能涉及直接复制他人文章的图文内容,证明他写得好。
本专栏将不可避免的产生:
- 致命笔误
- 直接复制
- 不懂装懂
- 懒得排版
- 证明显然
- 逻辑混乱
- 中式翻译
格的定义
格(Lattice),lattice是晶格的格,而非表格的格,前者更倾向于格状结构的“点”。
定义 1 格是 $\mathbb{R}^n$ 上的离散子群。
定义 2 由一组线性无关的向量(基) $\mathbf{B}$ 定义 $\mathbf{B}=\{\mathbf{b}_1,\cdots,\mathbf{b}_k | \mathbf{b}_i \in \mathbb{R}^n\}$,格是基 $\mathbf{B}$ 的线性组合的集合: $L(\mathbf{B})=\{\mathbf{B}\cdot \mathbf{x}| \mathbf{x}\in \mathbb{Z}^k\}$。
两种定义的等价性:
-
$2\to 1$ 是子群(封闭性,阿贝尔)+是离散的( $\exists\varepsilon$)。
-
$1\to 2$ 的证明没有前者那么显然:
离散子群 $\Lambda\subset\mathbb{R}^n$,假设该离散子群的生成空间是 $m$ 维的,如果 $m 定义一些概念便于表达: 定义 3 $\mathcal{P}(\mathbf{B}):=\mathbf{B}\mathbb{T}^n=\{ \Sigma_{i=1}^n x_i\cdot \mathbf{b}_i:\forall i.0\leq x_i <1 \}$,其中 $\mathbb{T}=[0,1)$ (基本域)。 $\overline{\mathcal{P}}(\mathbf{B}):=\{ \Sigma_{i=1}^n x_i\cdot \mathbf{b}_i:\forall i.0\leq x_i \leq1 \}$ 定义 4 $span(\mathbf{B})=\{\mathbf{Bx}:\mathbf{x}\in \mathbb{R}^n\}$ 首先找到一个格点和原点之间没有任何其他格点记为 $\mathbf{b}_1$ :以原点为球心,任意格点到原点的距离为半径划定一个超球体。由于离散性,在有限区域内的格点是有限的,此法总可以找到这样的点。 假设已经找到 $\mathbf{b}_1,\cdots,\mathbf{b}_i(i 定理 1 $\forall \mathbf{v}\in span(\mathbf{B})$ 都存在唯一的 $\mathbf{u}$ 和 $\mathbf{t}$,使得 $\mathbf{v}=\mathbf{u}+\mathbf{t}$,其中 $\mathbf{t}\in L(\mathbf{B})$,$\mathbf{u}\in \mathcal{P}(\mathbf{B})$。(带余除法) $\mathcal{P}(\mathbf{B}) + \mathbf{t}$ 是 $span(\mathbf{B})$ 的分割。实际上,任意区域 $S\subset span(\mathbf{B})$ 有 $\{\mathbf{x}+S:\mathbf{x}\in\mathbf{B} \}$ 是 $span(\mathbf{B})$ 的分割的都被称为基本域。 假设 $\exists\mathbf{v}\in\Lambda$ 且 $\mathbf{v}\notin L(\mathbf{B})$,存在唯一表示,$\mathbf{v}=\mathbf{u}+\mathbf{t}$,$\mathbf{u}\in\mathcal{P}\backslash\{0\}$。$\mathbf{u}=\sum_i{t_i\mathbf{b}_i}(0\leq t_i <1)$,体积 $vol(\overline{\mathcal{P}}(\mathbf{b}_1,\cdots,\mathbf{b}_{n-1},\mathbf{u}))=vol(\overline{\mathcal{P}}(\mathbf{b}_1,\cdots,\mathbf{b}_{n-1},t_i\mathbf{b}_n)) 一个格有不同的基,这些基有什么关系?显然,一个基可以由另一个基线性表出,但成倍放缩是不允许的,具体来说,两个基存在如下关系。 引理 1 格 $L$ 的两个基 $\mathbf{B},\mathbf{C}\in\mathbb{R}^{k\times n}$ 可以通过左乘一个特定的矩阵 $\mathbf{U}$ 相互转化。这个矩阵满足 $\mathbf{U}\in \mathbb{Z}^{k\times k}$ 且 $|det({\mathbf{U}})|=1$ (幺模矩阵)。 证明: 格具有两个不同的基 $\mathbf{C}$ 和 $\mathbf{B}$,基中的元素属于格,一定可由基的整数线性表出。即存在整数方阵 $\mathbf{U}$ 和 $\mathbf{V}$,使得 $\mathbf{B}=\mathbf{CU}$ , $\mathbf{C}=\mathbf{BV}$。$\mathbf{B}=\mathbf{CU}=\mathbf{BVU}$,由于 $\mathbf{B}$ 是单射,$\mathbf{I}-\mathbf{VU}=\mathbf{O}$ . $\mathbf{U}$ 是方阵,所以可逆,行列式为1:$\mathbf{U}^{-1}=\mathbf{V}$。 定义 1 幺模矩阵(unimodular matrix)是行列式绝对值为1的整数方阵。 引理 2 $\mathbf{U}$ 是幺模矩阵,那么 $\mathbf{U}^{-1}$ 是幺模矩阵。 更进一步的,引理1的强化版本。 定理 1 由基 $\mathbf{B}$ 和 $\mathbf{C}$ 表示的格 $L(\mathbf{B})$ 和 $L(\mathbf{C})$ 相等当且仅当存在幺模矩阵 $\mathbf{U}$ 有 $\mathbf{B}=\mathbf{C}\mathbf{U}$ 证明: $\gets$ $\to$ 引理1 定义 2 (整数)初等列变换(An elementary (integer) column operation on a matrix ) 初等列变换包括: 经过初等列变换的矩阵行列式绝对值大小是不变的,并且幺模矩阵经过整数基本列操作还是幺模矩阵。也可以说幺模矩阵本身就是一系列初等列变换。 定理 2 等价性:幺模矩阵 $\Leftrightarrow$ 初等列变换 证明: 设列初等变换 $\sigma$ 和幺模矩阵 $\mathbf{B}$ $\gets$ $\mathbf{B}$ 总可以表示为初等列变换,因为基本列操作总可以把矩阵化为上三角矩阵。因为幺模,故其对角元素只能是1和-1,所以总可以化为单位阵。(这里证明不完整,需要结合下面的引理3和定理3) $\to$ 初等列变换总可以表示为幺模矩阵 $\mathbf{B}$,对矩阵 $\mathbf{A}$ 做初等列变换: $\mathbf{I}$ 是幺模矩阵所以 $\sigma(\mathbf{I})$ 是幺模矩阵。 基本列操作的本质就是矩阵左乘一个幺模矩阵,现在可以自由的改变一个格的基了。那么是否有一个形式的基,所有的基都能唯一转化成该形式,以该基代表一个格? HNF(Hermite Normal form), $\mathbf{H}\in \mathbb{R}^{n\times n}$ 是HNF, $\mathbf{H}$ 需要满足: 引理 3 行向量 $\mathbf{v}=[v_1,v_2,\cdots,v_n]$ 可以通过一系列初等列变换变形为 $[0,0,\cdots,gcd(v_1,\cdots,v_n)]$ . 证明 数学归纳法,证明 $[v_1,v_2]$ 可以变形为 $[0,gcd(v_1,v_2)]$ .(辗转相除法) 定理 3 (HNF存在性唯一性) 任意非奇异矩阵 $\mathbf{B}\in\mathbb{Z}^{n\times n}$ ,都可以通过一系列基本整数列变换 $\sigma$ 变形为唯一的HNF. 证明: $n=1$ 显然成立,数学归纳法,假设 $n-1$ 时成立。 通过整数列变化 $\sigma$,有 $\mathbf{B}^\prime$ 是非奇异的,根据归纳法假设存在一系列整数列变化 $\sigma^\prime$ 使得 $\sigma^\prime(\sigma(\mathbf{B}))$ 是上三角矩阵,对角线元素大于0,只需要证明 $0\leq b_i < h_{ii}$ 存在。 从第 $n-1$ 行到第1行,如果 $0\leq b_i < h_{ii}$ 不成立,通过加减第 $i$ 列的整数倍(取余),总可以使条件达成,并且不改变 $b_{j}(j>i)$ 的元素。证毕。 HNF的存在性和唯一性可以判断两个基是否是同一个格,也可以判断向量是否属于格。 以 $\left(\begin{array}{c|c} 1 &33\\ 3&100\\ \end{array}\right)$ 和 $\left(\begin{array}{c|c} 1 &0\\ 0&1\\ \end{array}\right)$ 为基的格是相同的,显然后者基更好,然而HNF在某些情况的性质是不好的。 定理 4 任意正整数 $n$,存在一个矩阵 $\mathbf{B}=[\mathbf{b_1},\cdots,\mathbf{b_n}]\in \{-1,0,1\}^{n\times n}$ 有 $\|\mathbf{b}_i\|\leq \sqrt{n}$,使得其HNF $\mathbf{H}=[\mathbf{h_1},\cdots,\mathbf{h_n}]$,有所有的 $\|\mathbf{h}_i\|\geq 2^{\Omega(n)}$ . 证明
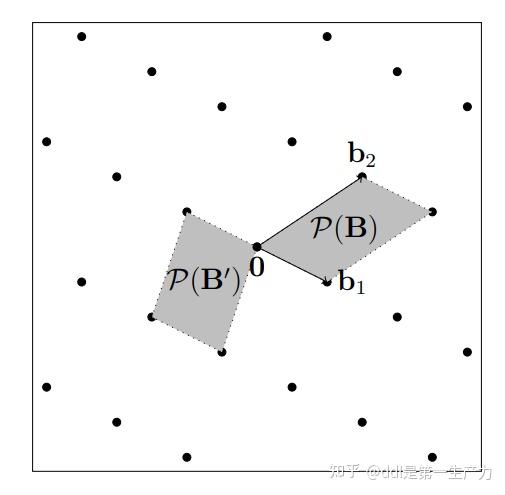
将后 $n-1$ 列加到第一列上,变为上三角阵: 后 $n-1$ 列 $\times-1$ : 爪型: 有 $\|\mathbf{h}_i\|>2^{n-2}$ 基可以施密特正交化,正交化后的矩阵具有一些性质(后面要用)。 正交化形式同线性空间中的施密特正交化,略。 定义 1(基本域): 给定基 $\mathbf{B}=[\mathbf{b_1},\cdots,\mathbf{b_n}]\in \mathbb{R}^{d\times n}$,其基本域为点集: 其中 $\mathbb{T}=[0,1)$。 推论 1 如果 $S$ 是格 $L(\mathbf{B})$ 的基本域,那么对于 $\forall x \in span(\mathbf{B})$,$S+x$ 也是基本域。 定义 2 基 $\mathbf{B}=[\mathbf{b_1},\cdots,\mathbf{b_n}]\in \mathbb{R}^{d\times n}$ 和其正交形式 $\mathbf{B}^*=[\mathbf{b_1}^*,\cdots,\mathbf{b_n}^*]$。格 $L(\mathbf{B})$ 的行列式:
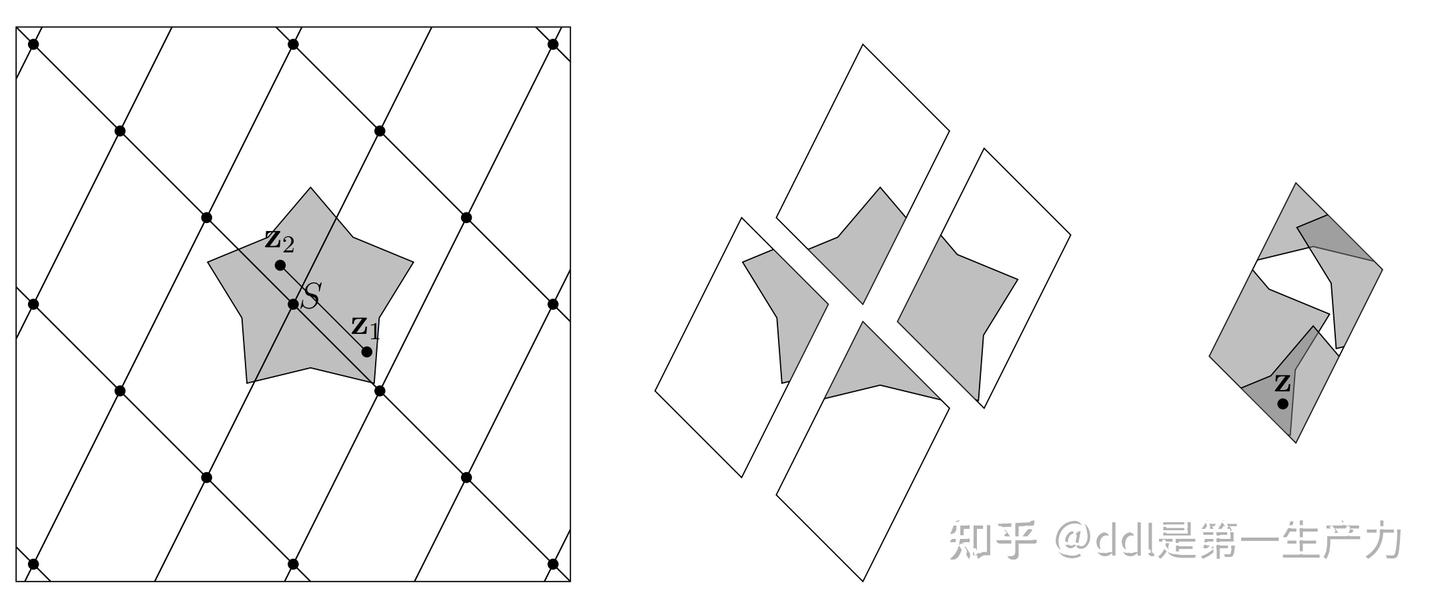
定理 1 (Hadamard 不等式) 当且仅当基正交时等号成立。 定理 2 基 $\mathbf{B}\in \mathbb{R}^{d\times n}$ 特殊地,如果基是非奇异方阵: 同一个格不同的基生成的不同的基本域,它们的体积是相同的 上图是格的基本域 $\mathcal{P}(\mathbf{B})$ 和 $\mathcal{P}(\mathbf{B'})$ 的示意图,$\mathbf{B'}=\{\mathbf{b_1-b_2},-\mathbf{b_2}\}$ 是 $\mathbf{B}$ 的一个基。 距离原点最近的格点是哪个?对于给定的一组基,在格中寻找这个最近的格点是一个很困难的问题。无法找到基的一种固定格式的转化让基的性质最好。(虽然HNF存在性和唯一性,但HNF在某些情况下是指数增长的,详见格密码1.2)。 定义 1 格 $\Lambda$ 的最小距离是两个格点的距离的最小值: 也可以用非0格的最小值表示: 两种定义是等价的,因为加法的封闭性。 下面介绍关于最短距离的困难问题: 定义 2 The Shortest Vector Problem,SVP: 给定一个格的基 $\mathbf{B}$,寻找最短距离的非零向量,即求解 $\|\mathbf{v}\|=\lambda(L(\mathbf{B})),\mathbf{v}\in L(\mathbf{B})\backslash\{0\}$。 距离 $\|\cdot\|$ 可以是任意形式的距离,在没有特别说明的情况下,本文的距离均为欧氏距离,欧式距离也是最常见的距离形式。 实际上SVP有许多变体: 定义 3 给定一个格的基 $\mathbf{B}$,$\forall \gamma\geq 1$,$\gamma$ 近似最短路径问题: 这些都是密码学困难问题(hard problems)。 本节估计 $\lambda$ 的上界,一个显然的上界是 $\min_i{\mathbf{b}_i}$,但这个上界与基的选取有关。 定义 1 Hermite factor of a lattice: $n$ 维格 $\Lambda$ 的赫米特因子是 $\gamma(\Lambda)=(\lambda(\Lambda)/det(\Lambda)^{1/n})^2$。$n$ 维赫米特常数是 $\gamma_n=\sup_\Lambda \gamma(\Lambda)$ 其中 $\Lambda$ 遍历$n$ 维所有的格*。 注意到,$\lambda(\Lambda)/det(\Lambda)^{1/n}$ 在线性放缩下是不变的,赫米特因子可以描述最小距离的上界。 定理 1 格 $\Lambda=L(\mathbf{B})$,集合 $S\subseteq span(\mathbf{B})$,如果 $vol(S)>\det(\Lambda)$,则存在 $\mathbf{z}_1,\mathbf{z}_2\in S$ 使得 $\mathbf{z}_1-\mathbf{z}_2\in \Lambda$。 如图,这是一件很 显然 的事。 容斥原理,必定存在重合的点 推论 1 Minkowski’s Convex body theorem,Minkowski 凸集定理: 格 $\Lambda$ 是满维度的,如果对称凸集 $S\subset\mathbb{R}^n$ 有 $vol(S)>2^n \det(\Lambda)$,那么它一定覆盖某个非零格点。 证明: 考虑集合 $S/2=\{\mathbf{x}:2\mathbf{x}\in S\}$,有 $vol(S/2)=2^{-n}vol(S)>\det(\Lambda)$.存在 $\mathbf{z}_1,\mathbf{z}_2\in S$ 使得 $\mathbf{z}_1-\mathbf{z}_2\in \Lambda\backslash\{0\}$。对称性可得,$2\mathbf{z}_1,-2\mathbf{z}_2\in S$,它们的线性插值$\mathbf{z}_1-\mathbf{z}_2$ 也属于 $S$.
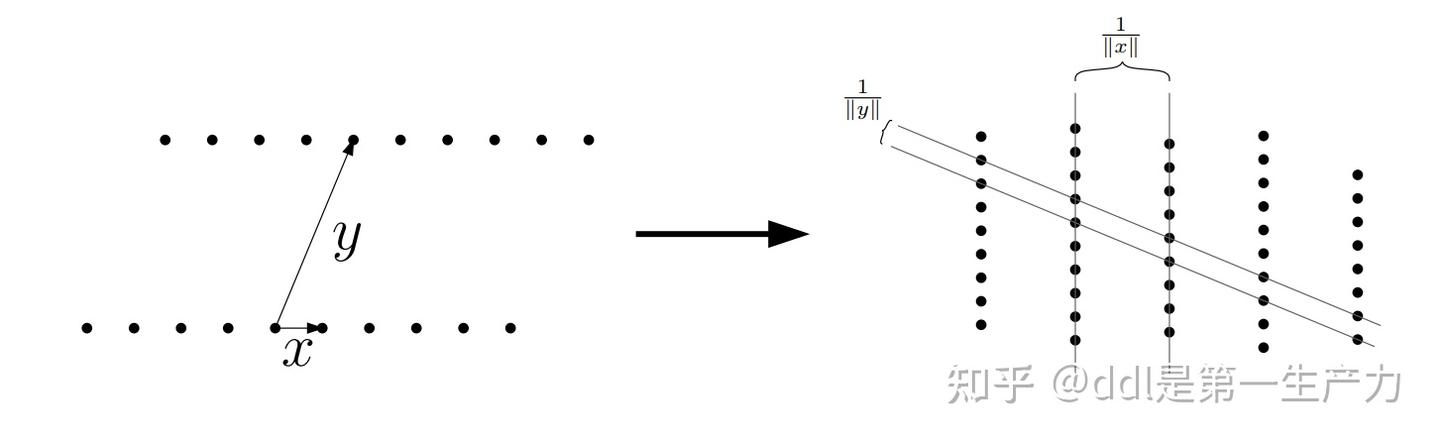
所以 $S$ 覆盖了非零格点 $\mathbf{z}_1-\mathbf{z}_2$. 推论 2 格 $\Lambda\subset\mathbb{R}^{n}$ 是满维度的,存在格点 $\mathbf{x}\in \Lambda\backslash\{0\}$,有 证明:反证法,任意格点有 $\|\mathbf{x}\|_{\infty}>\det(\Lambda)^{1/n}$。令 $l=\min\{\|\mathbf{x}\|_\infty\in\Lambda\backslash\{0\}\}$,$l>\det(\Lambda)^{1/n}$.超立方体$C=\{\mathbf{x}:\|\mathbf{x}\|_1 推论 3( Minkowski’s theorem**)** 赫米特常数最大是 $n$,对任意 $n$ 维格 $\Lambda$ 有非零格点 $\mathbf{x}$: 证明:均值不等式,$\|\mathbf{x}\|_2\leq \sqrt{n}\|\mathbf{x}\|_\infty$. 可以证明,无法渐进改进Minkowski界限,即存在常数 $c$,对任意的维度 $n$ 都存在 $n$ 维格子 $\Lambda_n$ 有 $\gamma_n>c\cdot n$。所以在常数因子意义下,$O(\sqrt{n})\det{(\Lambda)}^{1/n}$ 是包含行列式的最佳上界。因为 $\gamma_n$ 是 $O(n)$ 的,所以 $\frac{\|\mathbf{x}\|_2}{\det{\Lambda}^{1/n}}$ 是 $O(\sqrt{n})$ 的,我们找到 $\|\mathbf{x}\|_2$ 上界是 $\sqrt{n}\det{(\Lambda)}^{1/n}$,所以任意 $0 本节的主要内容是Minkowski’s theorem,这个定理找到了一个最短向量的非常重要的上界,这个上界与基的选取无关。但我们认识到,这个上界并不能帮我们解决SVP困难问题。例如基为 $(1,0)$ 和 $(0,d)$ 的格,最短距离是 $1$ 与上界 $\sqrt{2d}$ 相差很多。 我们也可以找到达到恰巧达到上界的格,寻找一个格 $\Lambda\subset \mathbb{R}^2$,有 $\gamma(\Lambda)=2/\sqrt{3}$,格如图所示。而且实际上 $\gamma_2=2/\sqrt{3}$,在之后的篇章,我们会知道达到赫米特常数的格的都会存在长度相等的基。 Hexagonal lattice 之前的章节中,我们用 $\lambda(\cdot)$ 代表一个格的最短向量的大小,如果用以原点为圆心的闭球的交集表示: 以 $\lambda$ 为半径的闭球(至少)包含了一个基,但如果包含多个格点有什么性质?我们知道 $\mathbf{v}$ 在球中 $-\mathbf{v}$ 也会在球中,所以我们考虑: 对任意 $n$ 维格 $\Lambda$,和一个正整数 $k \leq n$,令 $\lambda_k(\Lambda)$ 为包含至少 $k$ 个线性无关格点的最小的半径: 其中, 最短距离 $\lambda_1$ 是Successive Minima的首项,可以说这个定义推广了最短距离,Minkowski定理也可以进一步推广。 对任意格 $\Lambda$ 有 一些教材写的Minkowski第二定理中行列式的系数是 $\sqrt{n}$,我们知道 $\gamma_n \leq n$,所以上式更强。 证明: 格中存在线性无关的向量 $\mathbf{v}_i (i=1, \cdots, n)$,有 $\|\mathbf{v}_i\|_2 = \lambda_i$ ,考虑正交化后的向量 $\mathbf{v}_i^*$,并且定义变换: 我们要证明的是如下不等式: 不等式的前半部分是Minkowski定理,所以首先证明 $T(\Lambda)$ 的最短距离至少是1,即椭球 $E = \{\mathbf{x} \in \|T(\mathbf{x})\| < 1\}$ 有 $E \cap \Lambda = \{0\}$。 记格点 $\mathbf{x} \in \Lambda$ 和转换后的点 $\mathbf{y} = T(\mathbf{x})$,有 $\mathbf{x} = \sum_i c_i \mathbf{v}_i^*$,$\mathbf{y} = \sum_i \left(\frac{c_i}{\lambda_i}\right) \mathbf{v}_i^*$。寻找最大的 $k$,使得 $\lambda_k \leq \|\mathbf{x}\|_2 < \lambda_{k+1}$,那么有 $\mathbf{v}_1, \cdots, \mathbf{v}_k, \mathbf{x}$ 是线性相关的,所以可以只用 $\mathbf{v}_1, \cdots, \mathbf{v}_k$ 去表示 $\mathbf{x}, \mathbf{y}$。如果不线性相关,那么 $\|\mathbf{x}\|_2 = \lambda_{k+1}$,矛盾。(注意,若 $k=n$ 结论也成立): 证明后半部分(为什么我觉得相等。。。) 所有达到赫米特常数的格都具有相同长度的successive minima。 证明 从赫米特因子的定义可显然看出将每个基放缩成相同大小可以让分母的 $\lambda_1$ 最大。 在这里再放一遍赫米特因子的定义 $\gamma(\Lambda) = \left(\frac{\lambda_1(\Lambda)}{(\det\Lambda)^{1/n}}\right)^2$,赫米特常数 $\gamma_n$ 是 $n$ 维格的赫米特因子的上确界。 反证法,达到hermite常数的格不同的successive minima,寻找 $\lambda_i$ 对应的基向量 $b_i$,将 $b_i$ 放缩 $\{T(b_i)\}$ 仍然是线性无关的一组基,考虑 $\{T(b_i)\}$ 生成的格 $T(\Lambda)$ 的赫米特因子: 矛盾,证毕。 successive minima描述了格子“紧密性”如果successive minima增长的快,那么格子将会非常稀疏,计算SVP将会变得更困难。从定理2也看到了,如果successive minima增长的很慢,甚至都相等则可能会有一些较好的几何性质。successive minima还与后面的Packing Radius和Covering Radius 有关,也可以从信息编码的角度理解所谓“紧密性”。 高代泛函学的好的直接跳转对偶格。 对偶是用字数相等、结构相同、意义对称的一对短语或句子来表达两个相对应或相近或相同的意思的修辞方式。 在提及对偶空间的数学定义前,先思考一个小学问题——什锦糖。 什锦糖有 $n$ 种,数量分别为 $x_1, \cdots, x_n$ 个,价格分别为 $y_1, \cdots, y_n$,考虑总价函数 有了这个函数就可以计算某些数量下的总价。同样的,如果价格改变数量不变呢? 也具有一个类似的映射计算总价。不考虑现实意义,我们发现 $\mathbf{x}$ 和 $\mathbf{y}$ 的数学意义差不多,他们都是一些 $n$ 维向量,都可以找到一个映射($g_\mathbf{x}, f_\mathbf{y}$)与之对应。我们还发现: 不妨记总价为 $\langle \mathbf{x}, \mathbf{y} \rangle$。 函数与向量一一对应,函数空间和向量空间是同构的,我们可以用一个 $n$ 维向量表示函数,向量所在的空间是线性空间,所以函数可以由向量乘法抽象为线性函数: 设 $V$ 是数域 $\mathbb{P}$ 上的线性空间,$f$ 是 $V$ 到 $\mathbb{P}$ 的映射,称 $f$ 是 $V$ 上的线性函数,如果对任意 $\alpha, \beta \in V, k \in \mathbb{P}$ 满足: 设 $V$ 是数域 $\mathbb{P}$ 上的 $n$ 维线性空间,$V$ 上全体线性函数组成的集合记为 $L(V, \mathbb{P})$,对 $f, g \in L(V, \mathbb{P}), a \in V, k \in \mathbb{P}$ 定义加法和数乘: $L(V, \mathbb{P})$ 是数域 $\mathbb{P}$ 上的线性空间,称为 $V$ 的对偶空间,记为 $V^*$ . 设 $V$ 是数域 $\mathbb{P}$ 上的线性空间,$V^*$ 为其对偶空间,取 $x \in V$,定义 $V^*$ 上的函数 $x^{**}: x^{**}(f) = f(x), f \in V^*$ . $x^{**}$ 是 $V^*$ 上的线性函数,属于 $V^*$ 的对偶空间 $V^{**}$ . 设 $V$ 是数域 $\mathbb{P}$ 上的线性空间,$V$ 到 $V^{**}$ 的映射 $x \to x^{**}$ 是线性空间的同构映射。 固定映射,原像和像具有某种“映射”关系;同样地,当我们固定原像时,(线性)映射和像的关系不也是某种“映射”?原像和映射存在某种对称关系,我们将这种对称关系称为“对偶”。进一步抽象,将其所在(线性)空间抽象在一起,组成了对偶空间。实际上,对偶关系是对称的,相较于 $f(x)$,$ “全体线性函数组成的集合”这一概念显得抽象,因此我们常常用线性空间中的元素表示代表线性函数,即用向量表示。我们还知道 $n$ 维空间的对偶还是 $n$ 维空间,相同维度的线性空间是同构的,也可以不严谨地认为他们在一个空间中: 二维线性空间中一对基与对偶基 在了解了“对偶”的含义后,格作为作为离散群当然和线性空间有千丝万缕的关系,此时的数域变成了 $\mathbb{Z}$: 给定格 $\Lambda$,对任意 $\mathbf{y} \in \Lambda$,所有满足 $\mathbf{x} \in \text{span}(\Lambda)$ 且 $\langle \mathbf{x}, \mathbf{y} \rangle$ 是整数的集合称为对偶格,记为 $\hat{\Lambda}$ . 格和对偶格 根据对偶格的定义,有一些显然的结论。 格的对偶是格。(其实并不显然,详见定理 6) $\mathbb{Z}^n$ 的对偶格是 $\mathbb{Z}^n$ . $\forall c > 0$,$c \cdot \Lambda$ 的对偶是 $\frac{1}{c} \cdot \hat{\Lambda}$ . 任意两个格,如果有 $\text{span}(\Lambda_1) = \text{span}(\Lambda_2)$,则 $\Lambda_1 \subseteq \Lambda_2$ 当且仅当 $\hat{\Lambda}_1 \supseteq \hat{\Lambda}_2$ . 定理4、5揭示了格越密集,对偶格越稀疏。 原格的对偶格是子格的对偶格的子格 格 $L(\mathbf{B})$ 的对偶是以 $\mathbf{D} = \mathbf{B} \mathbf{G}^{-1}$ 为基的格,其中 $\mathbf{G} = \mathbf{B}^\top \mathbf{B}$,是 $\mathbf{B}$ 的gram矩阵。 证明:首先证明 $\mathbf{B} \in \mathbb{R}^{n \times n}$ 的情况。$\mathbf{v} \in \mathbb{R}^{n}$ 是对偶向量当且仅当与所有格向量乘积为整数,$\mathbf{B}^\top \mathbf{v} \in \mathbb{Z}^{n}$。即 $\mathbf{v} \in \mathbf{B}^{-\top} \mathbb{Z}^{n} = L(\mathbf{B}^{-\top})$,$\mathbf{B}^{-\top}$ 就是对偶格的基。 现在证明一般情况,任意向量 $\mathbf{D} \mathbf{y} \in L(\mathbf{D})$ 有: 所以 $\mathbf{D} \mathbf{y} \in \hat{L}(\mathbf{B})$,有 $L(\mathbf{D}) \subseteq \hat{L}(\mathbf{B})$,下证 $L(\mathbf{D}) \supseteq \hat{L}(\mathbf{B})$: 任意对偶格的向量 $\mathbf{v}$,根据定义有 $\mathbf{B}^\top \mathbf{v} \in \mathbb{Z}^k$ 并且 $\mathbf{v} \in \text{span}(\mathbf{B})$ 有: 格的对偶的对偶是自身,$\hat{\hat{\Lambda}} = \Lambda$ . 与线性空间的对偶不同,格的对偶是严格的自己,并非同构。要想证明定理7只需证明 $\mathbf{B} = \mathbf{D} (\mathbf{D}^\top \mathbf{D})^{-1}$,十分显然。 定理 7 再次体现了“对偶”这一关系的对称性,我们不妨称格和他的对偶格为一对对偶格,这时不必指定哪一个是原始格哪一个是对偶格,因为他们互相都可以唯一决定,而且他们的基也可以: 任意矩阵 $\mathbf{B}, \mathbf{D} \in \mathbb{R}^{m \times n}$,$\mathbf{B}, \mathbf{D}$ 是一对对偶格的基当且仅当满足: 基的对偶是唯一确定的,因此对偶基也可以唯一确定一个格,我们尝试用对偶基来表示原始格。事实上,格 $L(\mathbf{B})$ 可以定义为满足 $\mathbf{D}^\top \mathbf{x}$ 为整数向量的向量 $\mathbf{x} \in \text{span}(\mathbf{D})$ 的集合: 其中,$\mathbf{D}$ 是 $\hat{\Lambda}$ 的基。 通过定理8,有一些显然的推论: 一对对偶格的gram矩阵互为逆矩阵。 一对对偶格的行列式互为倒数。 任意整数格 $\Lambda \subseteq \mathbb{Z}^{d}$ 满足 $\hat{\Lambda} \subseteq \mathbb{Z}^{d} / \det(\Lambda)^2$;进一步地,如果 $\Lambda$ 是满秩的,有 $\hat{\Lambda} \subseteq \mathbb{Z}^{d} / \det(\Lambda)$ . 首先证明满秩情况,不失一般性的假设 $\mathbf{B} \in \mathbb{Z}^{d \times d}$ 是HNF,并且有对偶基 $\mathbf{D} = (\mathbf{B}^\top)^{-1}$。由于 $\mathbf{B}$ 是HNF,所以 $\mathbf{D}$ 的元素属于 $\mathbb{Z} / {\det(\mathbf{B})}$。(HNF详见 格密码 1.2) 然后证明一般情况,格 $\Lambda$ 和基 $\mathbf{B} \in \mathbb{Z}^{d \times n}$,对偶基 $\mathbf{D} = \mathbf{B} \mathbf{G}^{-1}$,考虑格 $L(\mathbf{G}^{-1})$ 的行列式: 因为 $\mathbf{G}$ 满秩,所以有 $L(\mathbf{G}^{-1}) \subseteq \mathbb{Z}^n / \det(\Lambda)^2$。又因为 $\mathbf{G}^\top \mathbf{G}^{-1} = \mathbf{I}$,有 $L(\mathbf{G}^{-1}) = \widehat{L(\mathbf{G})}$。 所以 $\widehat{L(\mathbf{B} \mathbf{G}^{-1})} \subseteq \mathbb{Z}^n / \det(\Lambda)^2$。 任意整数格 $\Lambda \subseteq \mathbb{Z}^{d}$,$\left((\det(\Lambda)^2 \cdot \mathbb{Z}^n) \cap \text{span}(\Lambda)\right) \subseteq \Lambda$;如果 $\Lambda$ 是满秩的,有 $|\det(\Lambda)| \cdot \mathbb{Z}^n \subseteq \Lambda$ 。 证明:引理1和定理5。 任何满秩的整数格 $\Lambda \subseteq \mathbb{Z}^n$ 在行列式模下是周期的。任意两个向量 $\mathbf{x}, \mathbf{y}$,如果有 $\mathbf{x} \equiv \mathbf{y} \pmod{\det(\Lambda)}$,则 $\mathbf{x} \in \Lambda$ 当且仅当 $\mathbf{y} \in \Lambda$。如果格的基非满秩,则将模改为行列式的平方。 施密特正交化将线性无关的向量组以此进行投影操作使其两两正交,定义投影操作: 将基 $\mathbf{B}$ 正交化: 注意到,$\mathbf{B}^*$ 不一定是格 $L(\mathbf{B})$ 的基。施密特正交化的形式不唯一,这与基向量的顺序有关。 基向量将原始格按层分割 基向量可以将格进行分割,分割成较低维度的子格的一些平移。并且这些较低维度的子格的距离是正交化向量的长度。 考虑投影格 的对偶。 $\mathbf{B}, \mathbf{D} \in \mathbb{Z}^{d \times n}$ 是一对对偶基,$\forall i = 1, \cdots, n$,$[\pi_i(\mathbf{b}_i), \cdots, \pi_i(\mathbf{b}_n)]$ 和 $[\mathbf{d}_i, \cdots, \mathbf{d}_n]$ 依然是对偶基。 证明:$i = 1$ 时,$\pi_1$ 不进行任何操作,显然。只需要证明 $i = 2$ 的情况下等式成立即可。定义 $\mathbf{B}^\prime = [\pi_2(\mathbf{b}_2), \cdots, \pi_2(\mathbf{b}_n)]$,$\mathbf{D}^\prime = [\mathbf{d}_2, \cdots, \mathbf{d}_n]$,要想证明对偶基需要证明: 根据对偶的对称性,如果我们定义一个相反顺序的投影操作 $\mathbf{d}^\dag_i$: 显然根据引理1,$[\mathbf{b}_{1}, \cdots, \mathbf{b}_i]$ 和 $[\tau(\mathbf{d}_{1}), \cdots, \tau(\mathbf{d}_i)]$ 是一对对偶基。 $\mathbf{B}, \mathbf{D} \in \mathbb{Z}^{d \times n}$ 是一对对偶基,$\forall i \leq j$,$[\pi_i(\mathbf{b}_i), \cdots, \pi_i(\mathbf{b}_j)]$ 和 $[\tau(\mathbf{d}_{i}), \cdots, \tau(\mathbf{d}_j)]$ 是对偶基。 $\mathbf{B}, \mathbf{D} \in \mathbb{Z}^{d \times n}$ 是一对对偶基,$\forall i$ : 特别地,$\mathbf{b}_n^* / \|\mathbf{b}_n^*\|^2 = \mathbf{d}_n$ . CVP (Closest Vector Problem) 是 SVP 的非齐次版本,是格困难问题之一。 给定格的基 $\mathbf{B}$ 和目标向量 $\mathbf{t}$,寻找格中的向量 $\mathbf{v}$ 使 $\|\mathbf{v} - \mathbf{t}\|$ 最小。$\gamma$-approximate CVP,在 $\gamma \geq 1$,寻找向量 $\|\mathbf{v} - \mathbf{t}\| \leq \gamma \cdot \text{dist}(\mathbf{t}, L(\mathbf{B}))$,其中距离函数是指 $\text{dist}(\mathbf{t}, \Lambda) = \inf \{\|\mathbf{v} - \mathbf{t}\| : \mathbf{v} \in \Lambda\}$。 CVP 也可以用任何范数定义,欧几里得范数是最常见的。通常,可以不失一般性的假设目标向量属于张成空间。因为考虑欧氏距离,如果不在张成空间中,目标函数也可以投影到空间上而不改变解。 格是子群,可以用商集 $\mathbb{R}^n / L$ 的元素表示格陪集。对于格 $L \subseteq \mathbb{Z}^n$,格的陪集为格的平移:$\mathbf{v} + L$,其中 $\mathbf{v} \in \mathbb{Z}^n$。 注意到格陪集可能不是格,因为陪集可能没有恒等元。CVP 可以等价于在格陪集 $\mathbf{t} + \Lambda$ 中解决 SVP 问题,近似解亦如此。 格陪集可以用对偶格表示,令 $\mathbf{D} \in \mathbb{R}^{n \times k}$ 是对偶格的一个基:$L(\mathbf{D}) = \hat{\Lambda} \subset \mathbb{R}^n$。$\forall \mathbf{t} \in \mathbb{R}^n$,称 $(\mathbf{D}^\top \mathbf{t}) \mod 1 \in [0,1)^k$ 为 $\mathbf{t}$ 关于 $\mathbf{D}$ 的校验子 (syndrome)。 $\mathbf{e} \in \mathbf{t} + \Lambda$ 成立当且仅当 $\mathbf{e}, \mathbf{t}$ 具有相同的校验子 $\mathbf{D}^\top \mathbf{e} = \mathbf{D}^\top \mathbf{t} \pmod 1$ 并且属于仿射张成空间 $\mathbf{e} \in \mathbf{t} + \text{span}(\Lambda)$。 当格是满秩的,$\mathbf{e} \in \mathbf{t} + \text{span}(\Lambda) = \mathbb{R}^n$ 显然成立,给定生成集和校验子可以唯一确定一个格陪集。所以在格陪集的 SVP 问题 (CVP) 可以表示为满足校验子的最短向量: 给定非奇异矩阵 $\mathbf{H} \in \mathbb{R}^{n \times n}$ 和一个校验子向量 $\mathbf{s} \in [0,1)^n$。寻找 $\mathbf{Hx} = \mathbf{s} \pmod 1$ 的最小范数解。在 $\gamma$ 近似版本中,目标是寻找与最优解相差不超过 $\gamma$ 倍的解。 目前没用有效的算法计算任意维度格SVP问题或仅计算最短向量长度。LLL算法是研究格SVP、CVP的重要算法。LLL算法可以在多项式时间内计算 $\gamma=2^{O(n)}$ 的近似解,适用于格的维度较小的情况。 基 $\mathbf{B}=[\mathbf{b}_1,\cdots,\mathbf{b}_n]\in\mathbb{R}^{m\times n}$ 是 $\delta-LLL$ 缩减基( $1/4<\delta<1$ ),需满足: 其中 $\pi_i$ 为正交操作:(见格密码1.7正交化) 投影操作 $\pi_{i+1}$ 可分为 $\pi_i$ 和 $\mu_{i+1,i}$ 两步,即先在前 $i-1$ 个基的方向投影,再在第 $i$ 个基的方向投影: 因此有的教材定义第二条可以写为: 当进行施密特正交化操作时,总是将剩余的基的方向抹去,这就导致正交基不是基。缩减基的动机就是保证尽量正交的同时,保留一部分其余基的方向,让这个基向量尽量的短以让基变短。所以每个 $|\mu_{i,j}|$ 都要小于等于 $\frac{1}{2}$。相当于对每个正交方向做带余除法,留下的余数。这一点在第二节深入探讨。 定义参数 $\alpha = 1/(\delta-1/4)\geq 3/4$,集合 $\{\|\mathbf{b}_i^*\|\}_i$ 的第 $k$ 小元素记为 $a_k$。 缩减基给了 $\lambda_i$ 的一些下界(见格密码1.5 s m) 给定 $1/4<\delta\leq 1$, $\mathbf{b}$ 是一个 $\delta-LLL$ 缩减基,有 $1\leq i\leq j \leq n$ : 证明: 定理1.1 定理1.2,1.4和1.5: 给定格,不妨设为 $n$ 维满秩格, $\lambda_i$ 对应的向量 $\mathbf{x}_i$, $\delta-LLL$ 缩减基 $\mathbf{b}$ 和缩减基的正交基 $\mathbf{b}^*$ 。则 $\mathbf{x}_i$ 可以被缩减基和正交基线性表出: 定义 $f(i)=\min\{j|r_{ij}\neq 0\}$,定义 $g(i)=\max\{f(j)|j=1,\cdots,i\}$。 所以 $r_{i{f(i)}}=r_{i{f(i)}}^*\geq 1$。 注意到,由于向量组 $\mathbf{x}_j(j=1,\cdots,i)$ 线性无关,组成向量组的基至少有 $i$ 个,所以: 又有,$g(i)\geq i$,由1.1: 定理1.3 1.2结合Minkowski定理 2017-07-25 Lenstra–Lenstra–Lovász (LLL) 算法是一种能将 lattice 顺便说一句:如果我有任何错误,请纠正我!在数学准确性和直观理解之间取得良好平衡是困难的,但我的目标不是公然犯错。如果我搞砸了,请随时在 tweet 上告诉我。这完全有可能。 如果你对以下内容没有一个很好的掌握,我认为 LLL 将很难理解(至少): 我写了另一篇关于 lattices 以及如何使用它们来构成非对称密码系统的博客文章。我认为先读那篇文章会很好,因为它涵盖了一些建议的背景知识。 LLL 经常被拿来与用于寻找 GCDs 的 Euclid’s Algorithm 进行比较。这是一个不完美的类比,但在高层次上,它们有一个核心的相似之处。也就是说,LLL 和 Euclid’s algorithm 都可以分解为两个步骤:“reduction”和“swap”。为了说明这一点,请看下面两种算法的伪代码: 如果你眯着眼看,你可以在伪代码中看到相似之处,但我认为核心思想是两种算法都使用了一种“先 reduce 后 swap”的技术来实现它们的目标。所以在这一点上,我们可以粗略地说,LLL 是 Euclid’s algorithm 的一个扩展,它适用于一组 就我个人而言,我觉得这个解释并不令人满意,但我能理解为什么它在建立理解的过程中可能有用。 另一个与 LLL 相似的算法是 Gram-Schmidt 正交化过程。在高层次上,Gram-Schmidt (GS) 接收一个 vector space 的输入 basis,并返回一个跨越相同空间的正交化(即 basis 中的所有 vectors 相互正交)的 basis。它通过利用 vector projections 将每个 vector “分解”为相关分量,并从所有 vectors 中移除冗余分量来实现这一点。如果 GS 对你来说不太好理解,我建议在继续阅读本文之前先去了解一下它。这个算法不仅与 LLL 相似,而且 LLL 还将 Gram-Schmidt 用作子程序。 你可能会说:“我们为什么不用 GS 来 reduce 我们的 lattice basis 呢?”我们不能,因为生活有时就是这么糟糕。GS 可能会让我们更接近我们想要的 basis,但 GS 不保证能产生构成我们 lattice basis 的正交 vectors。看这个: 注意到并非所有正交化的(灰色)vectors 都接触到了 lattice 的“点”吗?对我们来说幸运的是,GS 对于理解 LLL 仍然非常有用,所以这并非完全是损失。 除非你基本上是个女巫,否则我想你会发现从二维的 lattice basis reduction 开始会很有用。值得庆幸的是,我们有用于 reduce 二维 bases 的 Gauss’ algorithm。这很好,有几个原因: Gauss’ algorithm 定义如下: 我们来稍微分解一下。 我们首先将 然后我们计算我们新的 reduced vector 很酷,对吧?通过在 reduction 之前对 目前,我们只是挥挥手说 LLL 将 Gauss’ algorithm for reduction 扩展到可以处理 为了帮助理解 LLL 的工作机制,我们可以深入研究该算法的一个实现。这里有一些从 wikipedia 改编的 python 伪代码: LLL 非常简洁,但乍一看肯定有一些看似神奇的逻辑。让我们从 换句话说,假设 我们已经知道仅仅应用 GS 不一定会给我们一个 lattice 的 basis,但它确实给了我们“理想”的正交化矩阵。由于我们不能直接使用这个“理想”矩阵,我喜欢将 从 LLL 中分离出 length reduction 的伪代码,我们得到: 在第 1 行,我们建立两个变量: 外层循环条件在 length reduction 步骤中不那么重要,我们可以直接进入 length reduction 循环。length reduction 循环从第 length reduction 步骤基本上是 Gram-Schmidt’s reduction 步骤的微小修改。这是 LLL length reduction 步骤的另一种写法(省略 为了比较,这是 Gram-Schmidt vectors 的计算方式: 最后,在我们修改了我们的 basis 从我们的 Wikipedia 伪代码中提取“swap”步骤,我们得到: 在这一点上,算法已经完成了一轮 length-reduction。然后 LLL 必须确定接下来要关注哪个 vector。Lovász condition 将告诉我们是继续处理下一个 basis vector(第 3 行),还是将第 暂时不谈 Lovász condition 的含义,这个 swap 步骤让人联想到排序算法。回想一下, 那么 Lovász condition 本身呢?正如我早些时候所说,它基本上是一个确定 vectors 是否处于“良好”顺序的启发式方法。除此之外,很不幸我在这里没有太多要补充的,因为我的直观感觉仍然很模糊。Lovász condition 有多种等价的表示形式,没有一种让我感觉 100% 对头。到目前为止,我找到的最好的解释是这个 StackOverflow 帖子和“An Introduction to Mathematical Cryptography”。 “An Introduction to Mathmetical Cryptography” 讨论了 Lovász condition 的一个等价表示,即比较 basis vectors 在由一部分 basis vectors 张成的空间的正交补上的投影长度。 如果读到这里的任何人有关于一个相当直观的解释的链接,或者能以一种难忘的方式描述 Lovász condition,请告诉我! 如果你还没有建立起联系,Gaussian reduction 中的 事实上,一个新的 length-reduced vector 假设我们刚刚 reduce 了 我之前提到过,Gaussian two dimensional reduction 会使得 reduced vector 我发现来自“Mathematics of Public Key Cryptography” 的解释很好地说明了这一点。 最后,我们评论说,对于任何维度都存在一个自然的 Gaussian Reduction 的类似物。因此,尝试将 Lagrange-Gauss 算法推广到更高维度是很自然的。对于三维的推广已经由 Vall’ee 和 Semaev 给出。推广到更高维度会引入问题。例如,选择正确的线性组合来使用 b1,…,bn−1 size reduce bn 是在解决一个 sublattice 中的 CVP(这是一个难题)。此外,不能保证最终的 basis 在高维中实际上具有良好的属性。我们参考 Nguyen 和 Stehl’e 对这些问题的全面讨论以及一个在 3 维和 4 维中有效的算法。 LLL 是如何克服这个问题的?我倾向于认为 LLL 将一个 n 维问题分解为一系列二维情况,并一次处理一点点。这种技术,加上长度排序的近似,在实践中似乎效果很好。 再次,引用比我聪明的人的话: 正如我们在示例 16.3.3 中指出的,如果有一个正交或“足够接近正交”的 basis,lattices 中的计算问题可能会很容易。一个简单但重要的观察是,可以通过考虑 Gram-Schmidt vectors 的长度来确定一个 basis 是否接近正交。更准确地说,如果 Gram-Schmidt vectors 的长度没有下降得太快,那么一个 lattice basis 就是“接近正交”的。 感谢 Chris Bellavia 为这篇报告提供了宝贵的反馈。 满足 的格 $\Lambda$ 称为q阶随机格(q-ary random lattice)。(q是正整数) q阶随机格看起来很抽象,首先看看如何随机生成一个q阶随机格: 利用随机矩阵 $\mathbf{A}\in\mathbb{Z}^{n\times m}_q$ 的行向量的线性表出,得到q阶随机格: 和所有使 $\mathbf{Ax}=0$ 的格: 这两个东西是格的证明十分简单,离散且加法子群。 $q\mathbb{Z}^n$ 中的任意元素显然也属于这两个格,所以这两个格是q阶随机格。 奇妙的对偶关系 证明: $\forall \mathbf{y} \in \Lambda_q^\bot$ ,对 $\forall \mathbf{x} \in 1/q\cdot\Lambda_q$ ,有 即两个格的任意向量相乘为整数,定理一得证。(其中 $\mathbf{s}\in\mathbb{Z}^n_q$ ) 在本节中小括号 $(\cdot,\cdot)$ 代表矩阵或向量的垂直连接, $[\cdot,\cdot]$ 代表水平连接。 众所周知,解方程组 $\textbf{b}=\mathbf{A}^\top\mathbf{s}$ 是可以在多项式时间内解决的问题,但是加入小的噪声/扰动( $\mathbf{e}$ )后,问题就会变得十分困难。 给定任意矩阵 $\mathbf{A}\in \mathbb{Z}^{n\times m}_q$ : 其中 $\mathbf{s}\in\mathbb{Z}^n_q$ 是随机选取的向量, $\mathbf{e}\in\mathbb{Z}^m_q$ 是从“短”向量集合选取的向量。 从 中求解 $\mathbf{s}$ 就是LWE问题。 未完待续….
格密码1.2 基
格密码1.3 格与基本域
\documentclass{article}
\usepackage{tikz}
\usepackage{amsmath}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}[
scale=1.5,
point/.style={fill=black, circle, inner sep=1.2pt},
outerframe/.style={draw=gray, very thin} % Style for the focusing frame
]
% Define the basis vectors
\coordinate (O) at (0,0);
\coordinate (b1) at (1.6, -0.5);
\coordinate (b2) at (0.7, 1.1);
% Draw the focusing outer frame
\draw [outerframe] (-3,-3) rectangle (3,3);
% Draw the lattice points
\foreach \i in {-3,...,3} {
\foreach \j in {-3,...,3} {
\node at ($\i*(b1) + \j*(b2)$) [point] {};
}
}
% === Parallelogram P(B) ===
% Fill and draw the parallelogram
\filldraw [gray!50, draw=black, thick] (O) -- (b1) -- ($(b1) + (b2)$) -- (b2) -- cycle;
% Draw the basis vectors b1 and b2
\draw [-latex, thick] (O) -- (b1) node [midway, below right] {$\mathbf{b}_1$};
\draw [-latex, thick] (O) -- (b2) node [midway, above] {$\mathbf{b}_2$};
% Add the label P(B)
\node at ($0.5*(b1) + 0.5*(b2)$) {$\mathcal{P}(\mathbf{B})$};
% === Parallelogram P(B') ===
% Define the new basis B' = {b1' = b1-b2, b2' = -b2}
\coordinate (b1_prime) at ($(b1) - (b2)$);
\coordinate (b2_prime) at ($-1*(b2)$);
% Fill and draw the parallelogram
\filldraw [gray!50, draw=black, thick] (O) -- (b1_prime) -- ($(b1_prime) + (b2_prime)$) -- (b2_prime) -- cycle;
% Add the label P(B')
\node at ($0.5*(b1_prime) + 0.5*(b2_prime)$) {$\mathcal{P}(\mathbf{B'})$};
% Label the origin
\node at (O) [point, label={[label distance=-1mm]above right:0}] {};
\end{tikzpicture}
\end{document}
格密码1.4 最短距离与Minkowski’s theorem
一、问题定义
二、Minkowski’s theorem

格密码1.5 Successive Minima
格密码学基础
定义 1(Successive Minima)
定理 1 (推广的Minkowski定理)
定理 2
格密码1.6 对偶空间与对偶格
一、对偶空间
定义 1 (线性函数)
定义 2 (对偶空间)
定义 3 (对偶的对偶)
定理 1
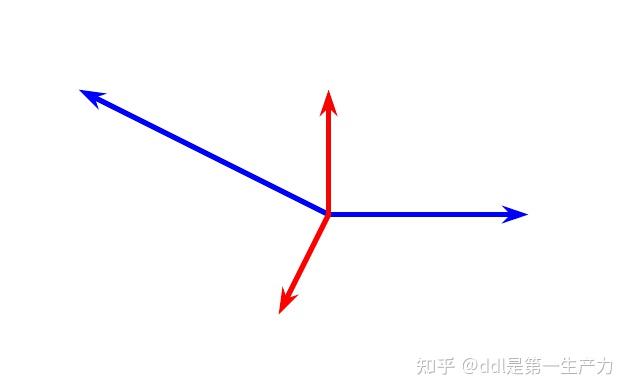
二、对偶格
定义 4 (对偶格)
定理 2
定理 3
定理 4
定理 5
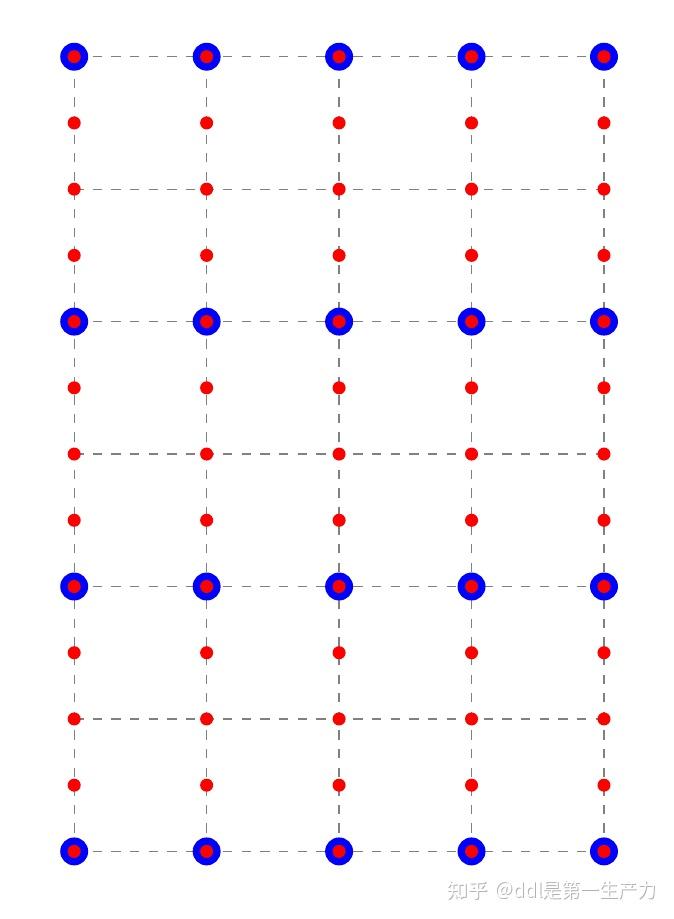
定理 6 (对偶基)
定理 7
定理 8
推论 1
推论 2
引理 1
定理 9
格密码1.7 基的施密特正交化及其对偶
一、施密特正交化
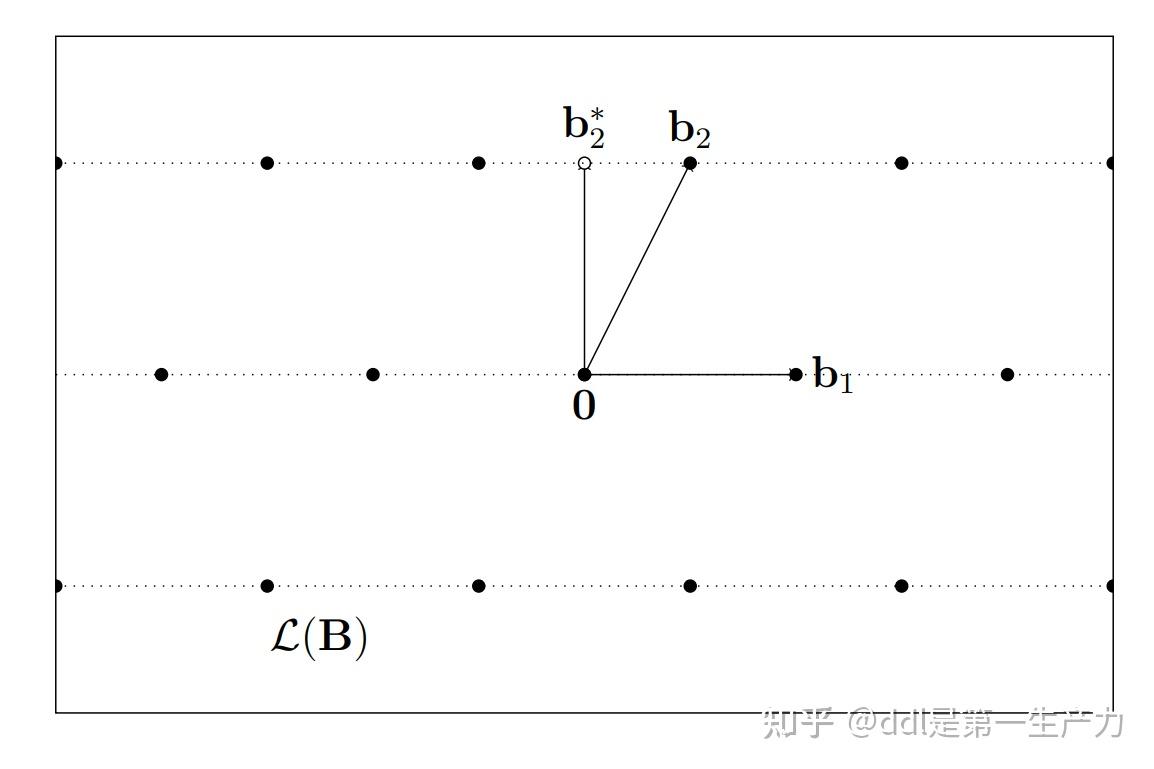
二、基正交化后的对偶
引理 1
$$
\text{span}(\mathbf{b}_1) \oplus \text{span}(\mathbf{B}^\prime) = \text{span}(\mathbf{B}) = \text{span}(\mathbf{D}) = \text{span}(\mathbf{b}_1) \oplus \text{span}(\mathbf{D}^\prime)
$$
$$
\begin{equation}
\nonumber
\begin{split}
\langle \pi_2(\mathbf{b}_i), \mathbf{d}_j \rangle &= \langle \mathbf{b}_i - \frac{\langle \mathbf{b}_i, \mathbf{b}_1 \rangle}{\langle \mathbf{b}_1, \mathbf{b}_1 \rangle} \mathbf{b}_1, \mathbf{d}_j \rangle \\
&= \langle \mathbf{b}_i, \mathbf{d}_j \rangle - \frac{\langle \mathbf{b}_i, \mathbf{b}_1 \rangle}{\langle \mathbf{b}_1, \mathbf{b}_1 \rangle} \langle \mathbf{b}_1, \mathbf{d}_j \rangle \\
&= \langle \mathbf{b}_i, \mathbf{d}_j \rangle \\
&= \delta_{i, j}
\end{split}
\end{equation}
$$定理 1
推论 1
格密码1.8 最近向量问题和格陪集(CVP and lattice cosets)
CVP (Closest Vector Problem)
定义 1
定义 2
定理 1
定义 3 校验子定义的 CVP 问题
格密码1.9 LLL缩减基(Reduced Basis)与LLL算法
LLL缩减基(LLL-Reduced Basis)
定义 1
定理 1
二、LLL算法
建立 Lattice Reduction (LLL) 的直观理解
L 的一个“坏” basis 高效地转换为同一个 lattice 的一个“相当不错”的 basis 的算法。这种将坏 basis 转换为更好 basis 的过程被称为 lattice reduction,它有很多有用的应用。例如,有一种针对利用有偏见的 RNGs 的 ECDSA 实现的攻击,可以恢复私钥。然而,我学习 LLL 工作原理的经历相当艰难。大多数关于 LLL 的材料似乎都是面向数学家的,我不得不(或者说我想要)花费大量时间来试图搞清楚该算法的直观感觉和工作机制。这篇博客文章是该过程的一个半组织化的大脑转储。我的目标是以一种逐渐减少“随手一挥”(hand-waving)的方式来介绍 LLL,所以你可以一直读到你对理解水平感到满意为止。建议的背景知识
LLL 与 Euclid’s Algorithm 的关系
def euclid_gcd(a, b):
if b == 0: # 基本情况
return a
x = a mod b # reduction 步骤
return euclid_gcd(b, x) # swap 步骤
# 先别尝试理解这个...
def lll(basis):
while k <= n:
for j in reverse(range(k-1, 0)): # reduction 步骤循环
m = mu(k,j)
basis[k] = basis[k] - mu*basis[j] # vector reduction
# 更新正交化的 basis
if lovasz_condition:
k += 1
else:
basis[k], basis[k+1] = basis[k+1], basis[k] # swap 步骤
# 更新正交化的 basis
k = max(k-1,1)
return basis
n-vectors 而不是整数。
LLL 与 Gram-Schmidt 的关系
sage: from mage import matrix_utils # https://github.com/kelbyludwig/mage; 使用 install.sh 脚本安装
sage: b1 = vector(ZZ, [3,5])
sage: b2 = vector(ZZ, [8,3])
sage: B = Matrix(ZZ, [b1,b2])
sage: Br,_ = B.gram_schmidt()
sage: pplot = matrix_utils.plot_2d_lattice(B[0], B[1])
sage: pplot += plot(Br[0], color='grey', linestyle='-.', legend_label='unmodified', legend_color='blue')
sage: pplot += plot(Br[1], color='grey', linestyle='-.', legend_label='orthogonalized', legend_color='grey')
sage: pplot
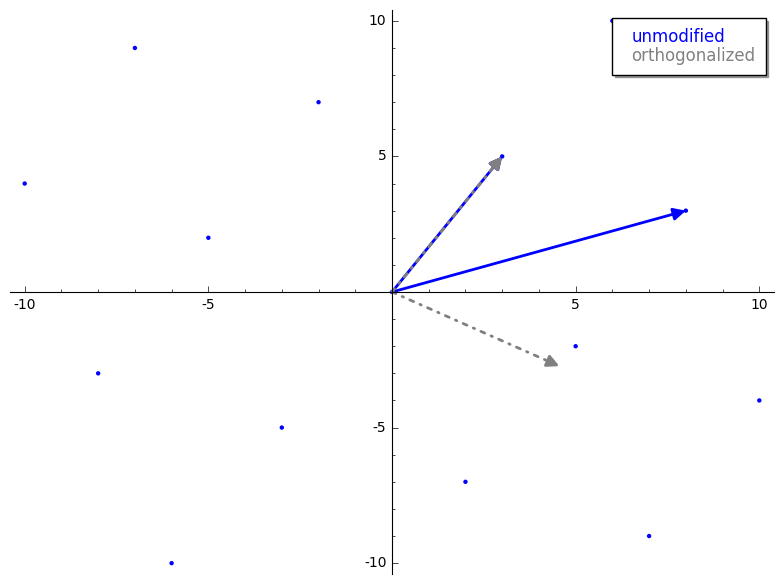
LLL 与 Gaussian Lattice Reduction 的关系
def gauss_reduction(v1, v2):
while True:
if v2.norm() < v1.norm():
v1, v2 = v2, v1 # swap 步骤
m = round( (v1 * v2) / (v1 * v1) )
if m == 0:
return (v1, v2)
v2 = v2 - m*v1 # reduction 步骤
gauss_reduction 接收两个代表我们 lattice basis 的 vectors。暂时忽略 while 循环,第一步是 swap 步骤。swap 步骤确保 v1 的长度小于 v2。除其他外,这将确保 gauss_reduction 的结果将按长度排序,这有助于一些证明来确保该算法良好工作。m 代表什么?m 是 v2 在 v1 上的标量投影(即较长的 vector 在较短的 vector 上的投影)。这与 GS 过程中产生的标量相同,但在 Gauss’s algorithm 中,我们将其四舍五入到最近的整数,以确保我们仍在处理 lattice 内的 vectors。这是一个重要的思想,让我们将这个过程可视化。v2 投影到 v1 上。这是投影后的 vector 在四舍五入前后的样子。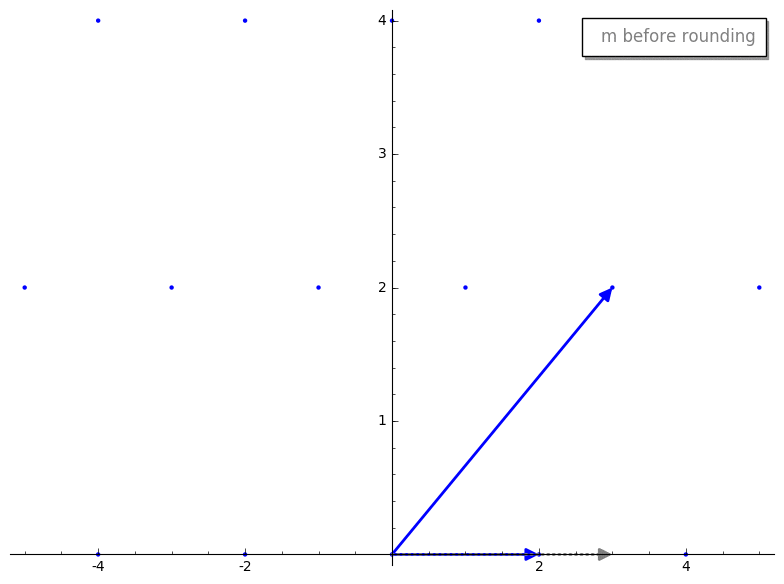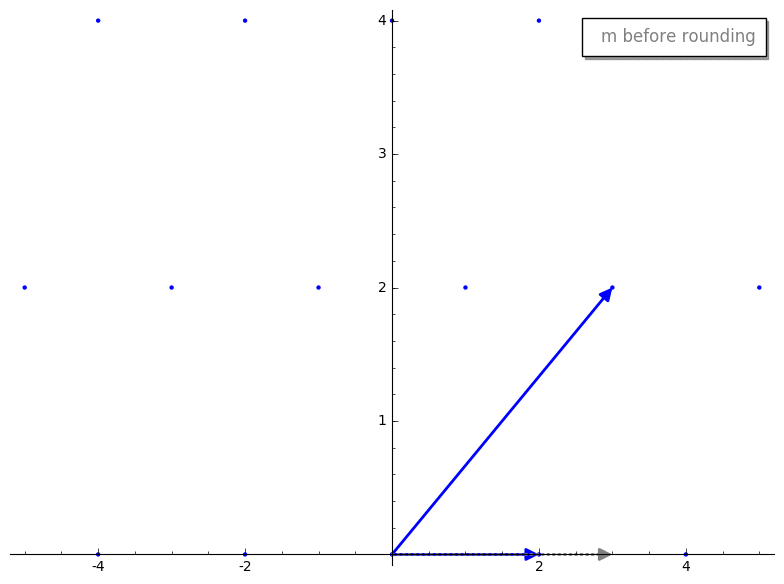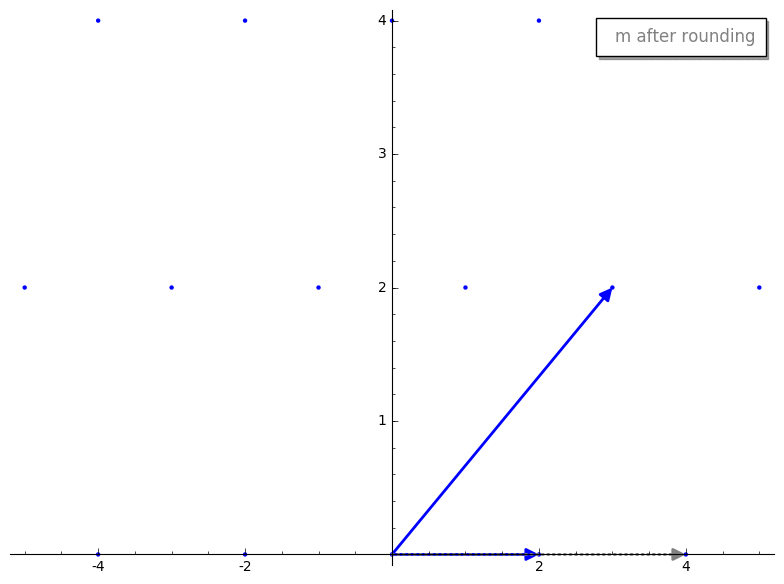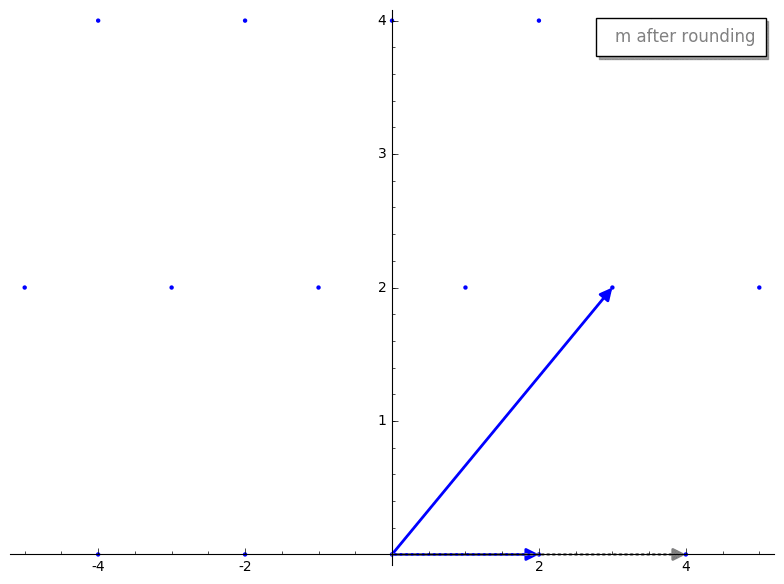
v2 - m*v1。这是在四舍五入 m 前后的 reduction 步骤。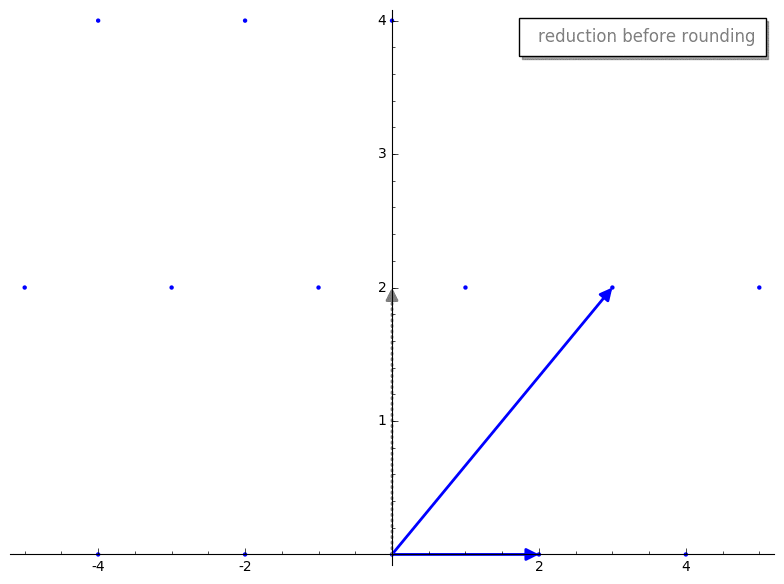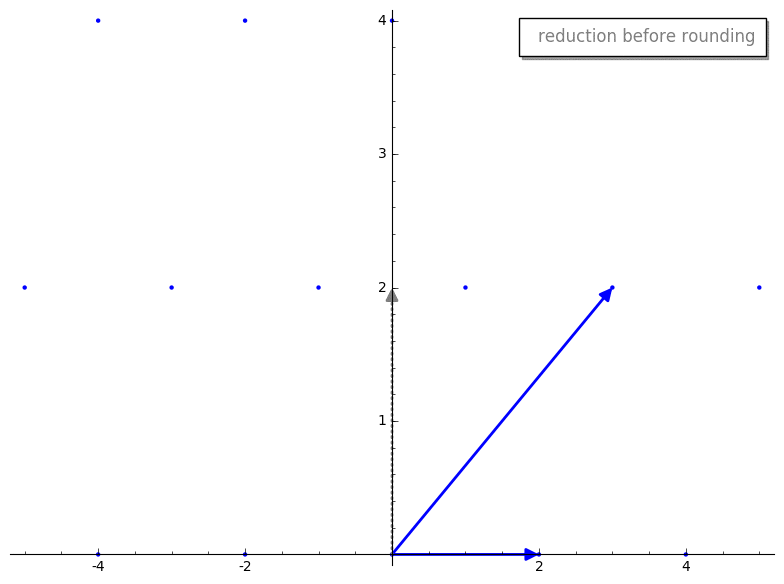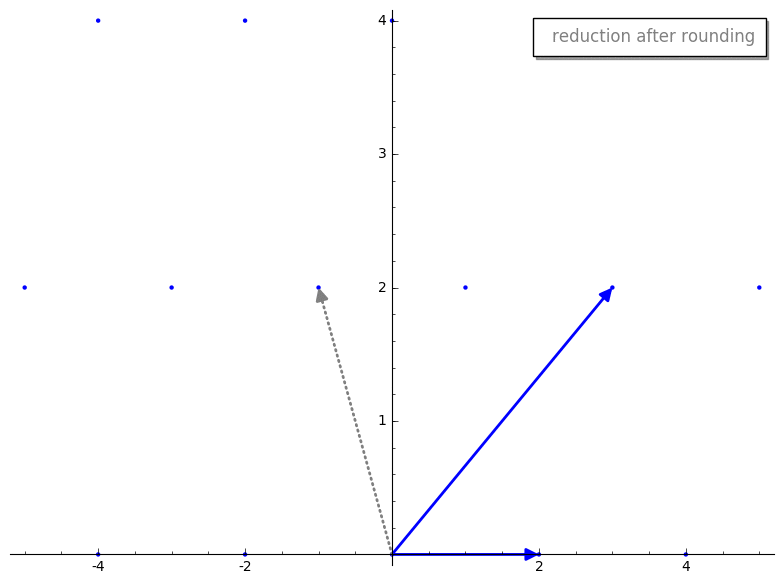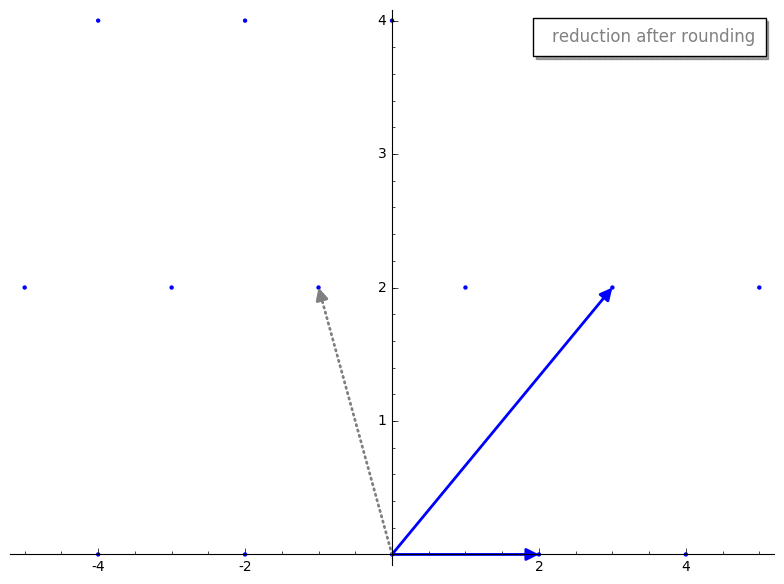
m 进行四舍五入,我们有点像“推倒”了我们新的 reduced vector v2,使其成为 basis 中的一个 vector。有趣的是,reduced v2 的长度似乎比原始 v2 短。这不是巧合,这是 reduction 步骤的保证!此外,最终的 basis vectors 将“几乎”正交,这正是我们想要的。我暂时不想用其工作原理的细节来纠缠任何人,但如果你不耐烦,可以跳到更技术性的解释。gauss_reduction 将会终止,并为二维 bases 返回一个“好”的(即短且几乎正交的)basis。
LLL tl;dr
n 个 vectors。在高层次上,LLL 遍历输入的 basis vectors,并对每个 vector 执行长度 reduction(在这一点上,这接近于 Gauss’ algorithm)。然而,我们处理的是 n 个 vectors 而不是仅仅两个,所以我们需要一种方法来确保输入 basis 的排序不影响我们的结果。为了帮助按长度对 reduced basis 进行排序,LLL 使用一种称为 Lovász condition 的启发式方法来确定输入 basis 中的 vectors 是否需要交换。LLL 在所有 basis vectors 都至少经历了一次 reduction,并且新的 basis 按长度大致排序后返回。
更深入地探讨 LLL
def LLL(B, delta):
Q = gram_schmidt(B)
def mu(i,j):
v = B[i]
u = Q[j]
return (v*u) / (u*u)
n, k = B.nrows(), 1
while k < n:
# length reduction 步骤
for j in reversed(range(k)):
if abs(mu(k,j)) > .5:
B[k] = B[k] - round(mu(k,j))*B[j]
Q = gram_schmidt(B)
# swap 步骤
if Q[k]*Q[k] >= (delta - mu(k,k-1)**2)*(Q[k-1]*Q[k-1]):
k = k + 1
else:
B[k], B[k-1] = B[k-1], B[k]
Q = gram_schmidt(B)
k = max(k-1, 1)
return B
mu 开始。mu
mu 是一个产生用于 vector reduction 的标量的函数。它类似于 Gram-Schmidt orthogonalization 和 Gaussian reduction 中的标量投影。唯一的主要区别是 mu 不是将一个 lattice vector 投影到另一个也在 lattice 中的 vector 上(像 Gauss’ algorithm 那样)。mu 是将一个 lattice vector 投影到一个 GS 正交化的 vector 上。B 是我们的输入 basis,Q 是对 B 应用 Gram-Schmidt(未归一化)的结果。由 mu(i,j) 产生的常数是第 i 个 lattice basis vector (B[i]) 在第 j 个 Gram-Schmidt 正交化 basis vector (Q[j]) 上的标量投影。下面的 GIF 是对 mu 的一个简短演示。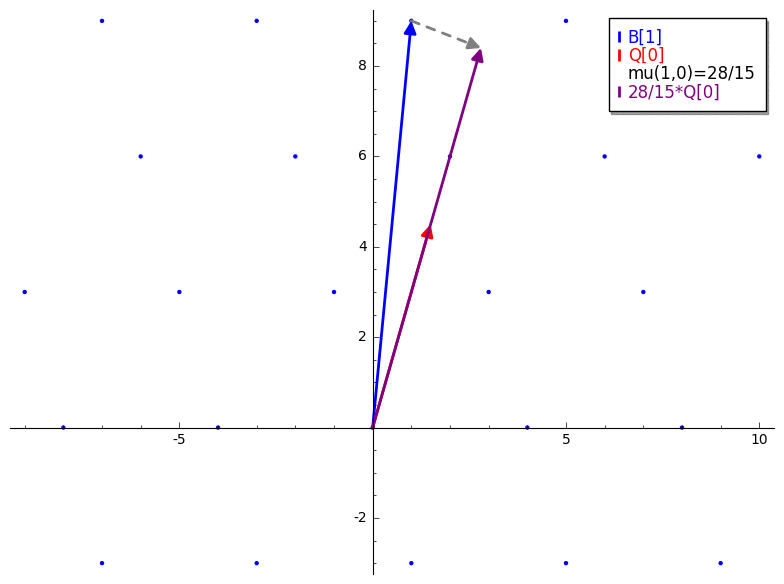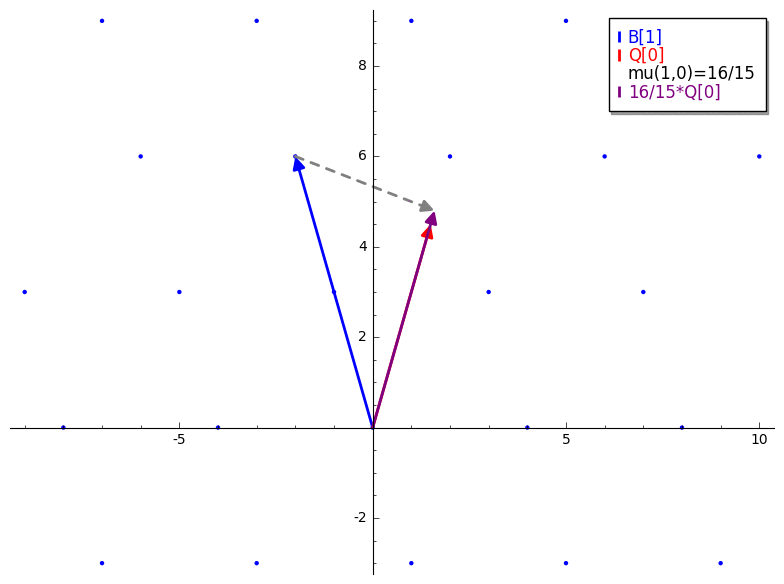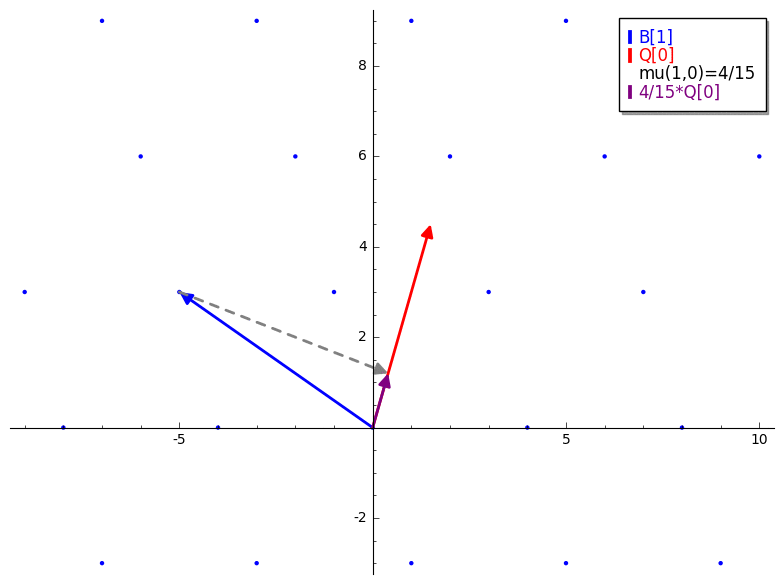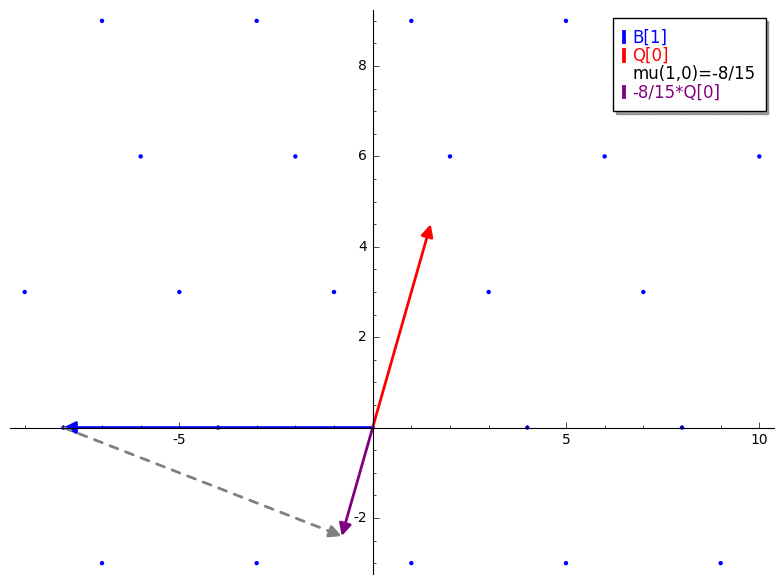
mu 看作是利用 GS 正交化矩阵作为衡量 reduction 成功与否的参考。Length Reduction
1. n, k = B.nrows(), 1
2. # 外层循环条件
3. while k < n:
4. # length reduction 循环
5. for j in reversed(range(k)):
6. if abs(mu(k,j)) > .5:
7. # reduce B[k]
8. B[k] = B[k] - round(mu(k,j))*B[j]
9. # 用新的 basis B 重新计算 GS
10. Q = gram_schmidt(B)
n: 一个常数,持有 basis B 的行数k: 记录我们正在关注的 vector 的索引k-1 个 basis vector 向第 0 个 basis vector 迭代,并检查 mu(k,j) 的绝对值是否大于 1/2。1/2 之所以重要,是因为我们正在对 mu(k,j) 的值进行四舍五入,如果其绝对值小于 1/2,那么我们将会减去一个零 vector,这不会 reduce vector。我们可以移除第 6 行的 if 语句,但这样在某些迭代中就会有多余的赋值(即 B[k] = B[k])。if 条件),针对 length reduction 循环中的每个 vector:B[0] = B[0]
B[1] = B[1] - round(mu(1, 0))*B[0]
B[2] = B[2] - round(mu(2, 1))*B[1] - round(mu(2, 0))*B[0]
...
B[k] = B[k] - round(mu(k, k-1))*B[k-1] - round(mu(k, k-2))*B[k-2] - ... - round(mu(k, 0))*B[0]
Q[0] = B[0]
Q[1] = B[1] - mu(1, 0)*Q[0]
Q[2] = B[2] - mu(2, 1)*Q[1] - mu(2, 0)*Q[0]
...
Q[k] = B[k] - mu(k, k-1)*Q[k-1] - mu(k, k-2)*Q[k-2] - ... - mu(k, 0)*Q[0]
B 之后,我们需要保持我们的正交化 basis 是最新的。在第 10 行,我们更新 Q。这绝对不是保持 Q 最新的最有效方法,但我只是从 Wikipedia 复制过来的,所以 ¯\_(ツ)_/¯。The Lovász Condition 和 Swap 步骤
1. # swap 步骤
2. if Q[k]*Q[k] >= (delta - mu(k,k-1)**2)*(Q[k-1]*Q[k-1]):
3. k = k + 1
4. else:
5. B[k], B[k-1] = B[k-1], B[k]
6. Q = gram_schmidt(B)
7. k = max(k-1, 1)
8.
9. return B
k 个 basis vector 放在 k-1 的位置(第 5-7 行)。k 是 LLL “正在关注”的 basis vector 的索引。假设 LLL 在第 k 个 vector 处,并且 Lovász condition 为真,那么 LLL 就移动到第 k+1 个 vector(第 3 行)。在这个阶段,LLL 基本上是在说从第 0 个到第 k 个 vectors 按长度大致排好序了(尽管这在下一轮 reductions 后可能会改变)。如果 Lovász condition 为假,第 k 个 basis vector 被放在 k-1 的位置(第 5 行),然后 LLL 重新关注(第 7 行)现在位于 k-1 位置的同一个 vector。再进行一轮 reduction,然后回到 swap 步骤。这就引出了描述 LLL 的另一种方式:LLL 是一个 vector 排序算法,它偶尔会通过使 vectors 变小来搞乱排序,所以它必须重新排序。
我在学习 LLL 时遇到的难题
Gaussian length-reduction 步骤是否保证提供短且几乎正交的 vectors?
m 值是 Gram-Schmidt 中 mu 值的最近整数。将 mu 的结果四舍五入并用作标量会产生一个好的 basis,这可能看起来不那么明显。在 Gram-Schmidt 中,使用 mu 的精确值可以实现 vector 的理想分解,这可以用来使 vector 相对于其他 basis vectors 正交化。而在 Gaussian reduction 中,我们对该结果进行四舍五入,这可能会影响正交性。幸运的是,即使在四舍五入 mu 之后,length reduction 步骤也会产生“几乎正交”的 vectors。B[k](其中 B[k] = B[k] - round(mu(i,j))*B[j])与 B[j] 的夹角将始终在 60 到 120 度之间。这个保证源于另一个事实,即 B[k] 在 B[j] 上的投影将始终位于 -1/2*B[j] 和 1/2B[j] 之间。为什么后一个事实是真的?直观上,我们已经从 B[k] 中移除了所有可能的 B[j] 的整数分量,因此,B[k] 在 B[j] 上的最终投影必须位于 -1/2*B[j] 和 1/2B[j] 之间。B[k],所以我们知道 B[k] 在 B[j] 上的投影将位于 -1/2*B[j] 和 1/2*B[j] 之间。使用 vector projection 的定义(见下图),我们可以重写我们的不等式: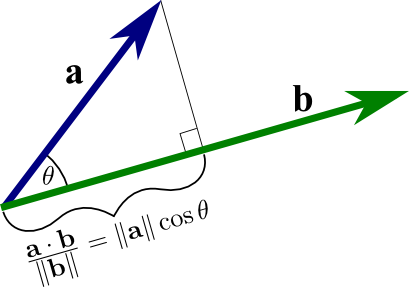
|B[k]|*cos(theta) = proj B[k] onto B[j]
=>
|B[k]|*abs(cos(theta)) <= 1/2*|B[j]|
(|B[k]|/|B[j]|)*abs(cos(theta)) <= 1/2
B[k] 比 B[j] 短(在“Introduction to Mathematical Cryptography”中有证明)。根据这个 StackOverflow 帖子,这两个事实证明了输出 vectors 的“几乎”正交属性。我实际上不 100% 确定这些证明是正确的(我认为他们犯了一个错误,但我也没有证明),所以我不能说得更多。为什么 Gaussian lattice reduction 不容易推广到处理超过 2 个 vectors 的 lattices?
LLL 是如何使用 GS 作为指导的?
References:
格密码1.10 q阶随机格、LWE和BDD
一、q阶随机格
定义1
定理 1
二、LWE和BDD
定义 2 Learning With Errors(LWE)